洛希极限

概述

传统惯性参考系：传统观点认为静止或者匀速直线运动的参考系或者牛顿第一定律成立的参考系。
广义惯性系：在一个引力场中做自由运动且不旋转的参考系是惯性参考系。
惯性力：速参考系中应用牛顿定律所产生的一个虚拟力，指的是物体所受的虚拟力。

示例：

在一个加速运动的火车上的人。

• 地面参考系：车停止则人停止；
• 火车参考系：存在惯性力，大小 $F=ma$ ，方向和火车方向相反；

潮汐力

潮汐力是由于一个天体（如月球或太阳）对另一个天体（如地球）不同部位的引力差异而产生的力。这种力导致了海洋潮汐等现象。
场景

地球被木星吸引，描述在地球上的个人受力；

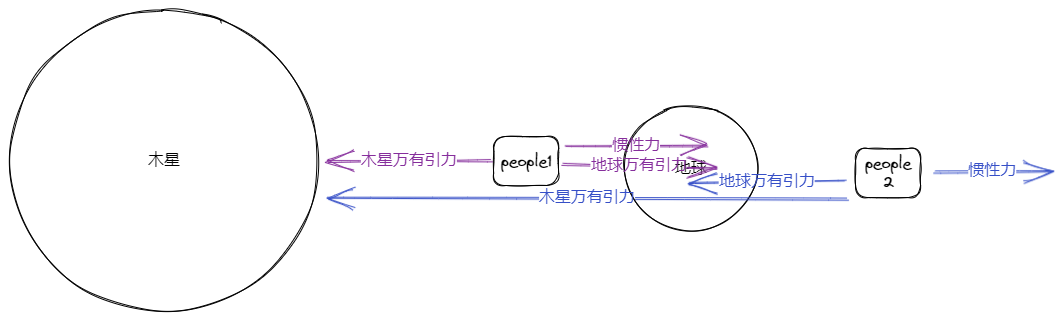
一个人的受力： $F=地球万有引力+木星万有引力+惯性力$ ；
潮汐力大小： $F=木星万有引力+惯性力$ ；

• People1：木星引力>惯性力；
• People2：木星引力<惯性力；

洛希极限

洛希极限：当小天体所受到的潮汐力=自身的引力时，之间的距离称之为洛溪极限。

刚体洛希极限计算公式， $\rho_{M}$ 代表大天体密度； $\rho_{m}$ 代表小天体密度； $R_{M}$ 代表大天体半径。

$$r=1.26 \times \sqrt[3]{\frac{\rho_{M}}{\rho_{m}} } \times R_{M}$$

流体洛希极限计算公式， $\rho_{M}$ 代表大天体密度； $\rho_{m}$ 代表小天体密度； $R_{M}$ 代表大天体半径。

$$r=2.44 \times \sqrt[3]{\frac{\rho_{M}}{\rho_{m}} } \times R_{M}$$

应用

土星光环

土星光环：科学家认为一颗彗星被土星潮汐力撕碎了，形成了光环。

苏梅克列维 9 号

苏梅克列维 9 号于 1992 年被木星潮汐力撕碎，1994 年与木星相撞。

流浪地球

假设地球是一个刚体，那么他的洛希极限是5.6WKM，比木星的半径7.15WKM 要小，这说明地球必须进入木星才会被潮汐力撕碎。假定地球是一个流体，那么它的洛希极限是10.9WKM。由于地球既不是流体也不是刚体，所以他和木星的洛希极限应该在5.6WKM和10.9WKM之间。

Moss 给出的洛希极限其实是太阳和木星的（89WKM和171WKM），而不是地球和木星的。